Yona Friedman, Spatial City, project Perspective, 1958-59

Yona Friedman, Spatial City, project Perspective, 1958-59. © 2007 Artists Rights Society (ARS), New York / ADAGP, Paris

Proportion and Perspective
Steven Wills, Coordinator, Wachovia Education Resource Center, Philadelphia Museum of Art 

This image group is meant to supplement a lesson in a middle-school math class that deals with measurement and proportion — usually in the context of geometry. There are several purposes of the image group, specifically:

  • to help visual learners see how the concepts discussed in class can be applied;
  • to help answer the question: “Why do we have to learn this?” (A frequent question in a math class); and
  • to help show the connections between math and science and math and art, thus helping to build an interdisciplinary approach to teaching.
Constantinople, Christ the Saviour in Chora, Vault; Presentation of the Virgin in the Temple; detail of Joachim, Anne, Mary, High Priest Zacharias, and the Holy of Holies, c. 1310-21. Image and original data provided by Erich Lessing Culture and Fine Arts Archives/ART RESOURCE, N.Y. http://www.artres.com/
Catena (Vincenzo di Biagio), The Adoration of the Shepherds, probably after 1520. Image © The Metropolitan Museum of Art
Diagram Demonstrating Filippo Brunelleschi’s Perspective Technique from a Lost Painting of the Battistero di San Giovanni. Image and original data provided by SCALA, Florence/ART RESOURCE, N.Y.; artres.com; scalarchives.com; (c) 2006, SCALA, Florence/ART RESOURCE, N.Y.
Albrecht Altdorfer, Saint Sebastian Altar; Christ before Caiphas, c. 1509-1516. Image and original data provided by Erich Lessing Culture and Fine Arts Archives/ART RESOURCE, N.Y. http://www.artres.com/

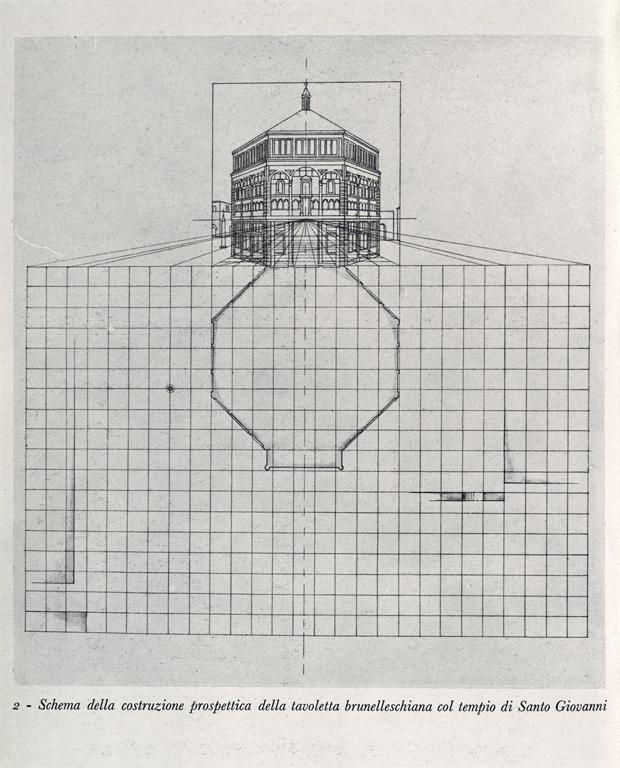
The introduction of three-dimensional space in geometry (moving from square feet to cubic feet, for instance) traditionally devolves into a recitation of mathematical formulae — to be memorized and drilled. There are, of course, many applications of three-dimensional geometry that should be introduced to supplement these formulae, but the history of art offers a unique approach. Simply put, how does an artist present a realistic three-dimensional view on a two-dimensional surface? While the use of linear perspective seems basic to realistic painting, it was not seen before the 1400s. Some of the images in the image group are selected to show this transition — using similar scenes or topics depicted prior to the use of perspective and after. These comparisons will reveal the power of the basic geometric “discovery.” Additional images are provided to show how artists can use perspective in a more playful sense — creating illusions and “tricking” the observer with impossible realities.

A complementary discussion of proportion helps round out the application geometry in art. One cannot depict reality (in the days before photography) without understanding the intricate measurements and ratios of objects, people, etc. The image group includes several sketches and studies made by classical artists seeking to represent reality on their canvases. A few of these sketches seem very much like computer renderings — revealing the connections between an understanding of proportion and, for example, a realistic computer game or CAD program. Furthermore, since CAD is basic for design and engineering, the applications offer great breadth and depth.

Students do not learn well through “drill and kill,” and we see the results of this in our national mathematics competency scores. An approach that involves visual application is sorely needed across the curriculum — and this can be one piece of it.

This essay was the winner of a 2010 Artstor Travel Award.